
いよいよコーシーの積分定理について述べていきます。ここでは主に解析概論の57. コーシーの積分定理、に基づいて記載しています。
前回、原始関数を使った積分計算の定理を紹介しました。この定理から、ある関数の積分の計算は原始関数がある場合はそれを求めて、$C$の終点と始点での$F$の値の差で計算できることがわかりました。特に$C$が閉曲線の場合$w_0=w_1$なので
$$\int_C f(x) dx=F(w_1)-F(w_0)=F(w_0)-F(w_0)=0$$
でした。
原始関数を使った積分計算の定理にしろ、上記の等式にしろ、被積分関数$f$に原始関数があればそれを使って計算できる、という話でした。
一方、この記事で扱うコーシーの積分定理は原始関数(の存在)には言及せずに似たような結論を主張します。積分路及び積分路を含む集合に条件をつけることで同様な結論を得ることができます。
コーシーの積分定理(解析概論より):領域(連結な開集合)$K$で正則な関数$f$について、単純閉曲線$C$でその周も内部も$K$に属しているとき、次式が成り立つ
$$\int_C f(x) dx=0$$
コーシーの積分定理で検索すると、他にも積分路$C$を含む領域が単連結とか可縮とか、積分路が三角形とか円周とか色々な条件が登場します。非積分関数に関する条件は「正則」に統一されています。
全てを包括する条件で1つ示すとすると「単連結」という概念を導入して次のような形で定理が成り立ちます。
単連結の定義:領域$K$が単連結であるとは、$K$上の全ての単純閉曲線についてその内部の各点が$K$に属すること。
コーシーの積分定理(単連結領域版):単連結な領域$K$で正則な関数$f$と$K$内の単純閉曲線$C$について次式が成り立つ。
$$\int_C f(x) dx=0$$
追記:単連結領域$K$で正則な関数$f$には$K$の全域で原始関数が存在する。
コーシーの積分定理が成り立てばそこから原始関数を作ることができます。したがって追記の部分も成り立ちます。解析概論の57. コーシーの積分定理の最後の段落に上記の単連結領域版の記載があります。
コーシーの積分定理が成り立たない場合を1つ示しておきます。
$f(z)=\frac1{z-a}, C=\{z|\, |z-a| = R\}$とすると$z=a$で$f$は正則ではありません。従って定理の前提は成り立ちません。この時、
$$\int_C \frac1{z-a} dz=2\pi\,i$$
となり、ゼロではありません。計算は置換積分で求まります。やってみましょう。$z-a=R\,e^{i\,\theta}\,(\theta: 0 \to 2\,\pi)$と置換します。両辺を$\theta$で微分すると、$\frac{dz}{d\theta}=R\,i\,e^{i\,\theta}$となります。すると
$$\int_C \frac1{z-a} dz=\int_0^{2\,\pi} \frac1{z-a}\frac{dz}{d\theta}d\theta=\int_0^{2\,\pi}\frac1{R\,e^{i\,\theta}}R\,i\,e^{i\,\theta}d\theta=\int_0^{2\,\pi}\,i d\theta=2\pi\,i$$
またコーシーの積分定理を次のように拡張することができます。
拡張:単純閉曲線$C$の内部に単純閉曲線$C'$があり、その間の環状の領域に$C, C'$を加えた領域で$f$が正則であるとき、次式が成り立つ。
$$\int_C f(z) dz=\int_{C'} f(z) dz$$
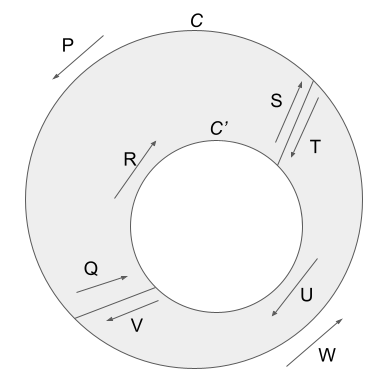
外側の円が$C$、内側の円が$C'$で、灰色の部分で関数$f$が正則ですから、単純閉曲線$P\to Q \to R \to S$に沿った積分はコーシーの積分定理より0, $T\to U\to V\to W$に沿った積分も0です。両方の積分を足してみると$P$から$W$までの弧に沿った積分を全部足し合わせることになりますが、途中$Q$と$V$、$S$と$T$はそれぞれ打ち消し合うことから$P\to W$の積分路と$U \to R$の積分路が残ります。それらは外側の円$C$と内側の円の逆向き$-C'$です。その和がゼロですから、
$$\int_C f(z) dz + \int_{-C'} f(z) dz=\int_C f(z) dz - \int_{C'} f(z) dz=0$$
次回はコーシーの積分表示に進みます。
