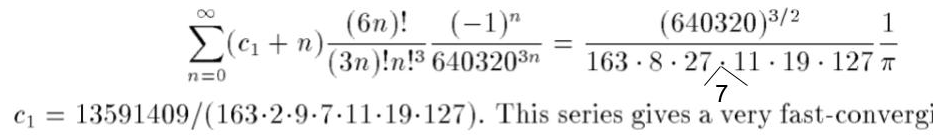コロナ対策の一環で3月初旬から在宅勤務をしています。今は世の中に貢献できることが、「家にいて病気にならないこと」、だけなので、それを実践しています。医療関係の方々のみならず、社会インフラを動かすために出勤される皆様には敬意を表します。
平日も多少時間の余裕ができたため、以前このブログで書いた楕円曲線シリーズを読み直し、そこで参照した文献を眺めておりました。
この中であげた、
Francois Morain, Introduction to Complex Multiplication,
http://algo.inria.fr/seminars/sem94-95/morain.ps
がわずか4ページで、ワイエルストラスのペー関数から初めて、j不変量を導入し、2次形式と判別式と類群と類数とヒルベルト類多項式を導入し、さらに虚数乗法を定義します。そして虚数乗法の応用を3つ、1)楕円曲線による素数判定法、2)類数問題、3)ラマヌジャンを紹介しています。
ラマヌジャンが発見した\(\frac{1}{\pi}\)の公式の証明に虚数乗法が使われる、ということで、その公式も記載されていました。
こんな凄い式をラマヌジャンは知っていたんだ!と感激しながら、せめて数値計算でこの式が成立することを確認しようと、まず左辺をmaximaに打ち込んでみました。チラッとvery fast-convergingとあるので、とりあえず総和の上限\(\infty\)を2,3,4と置き換えて数値計算させて収束の様子を見ると、0.02493195446879306に収束したように見えます。
一方右辺はただの四則計算です。maximaに入力して数値計算させてみると0.1693295241005528、、、、違いすぎます。入力式を、目を皿のようにして眺めても合っています。
失礼ではありますが、論文著者が転記ミスをしているのだろうと勝手に予想して、この式の正しいバージョンをネットで探し始めました。するとこんな楽しい論文が見つかりました。
Ramanujan’s Series for 1/π: A Survey,
Nayandeep Deka Baruah, Bruce C. Berndt, and Heng Huat Chan
https://faculty.math.illinois.edu/~berndt/articles/monthly567-587.pdf
この論文はインド数学会が発行するMathematical Studentという雑誌に掲載されたものを許可を得て著者が再配布しているものだそうです。
ラマヌジャンに始まり、1/πに収束する級数の歴史を辿りながら、その数学的背景及び様々な逸話を紹介する、という趣向の論文です。本記事では1/π論文と呼ぶことにします。
この1/π論文は、ラマヌジャンが英国で最初に発行した論文で述べた3つの式から始まります。これら3つにはpochhammer(x,n)関数が使われています。これはxを実数、nを自然数として\(x\,\left(x+1\right)\,\left(x+2\right) \cdots \left(x+n\right)\)を計算する関数です。xから始まる"階乗"という感じでしょうか。そして共通な部分式\(A_n\)を定義します。
(%i1) A[n]:=pochhammer(1/2,n)^3/(n!)^3;
$$ \tag{%o1} A_{n}:=\frac{\left(\left(\frac{1}{2}\right)\right)_{n}^3}{n!^3} $$
ここから3つの公式が提示されます。
(%i2) 4/%pi=sum((6*n+1)*'(A[n])/4^n,n,0,inf);
$$ \tag{%o2} \frac{4}{\pi}=\sum_{n=0}^{\infty }{\frac{\left(6\,n+1\right)\,A_{n}}{4^{n}}} $$
(%i3) 16/%pi=sum((42*n+5)*'(A[n])/2^(6*n),n,0,inf);
$$ \tag{%o3} \frac{16}{\pi}=\sum_{n=0}^{\infty }{\frac{\left(42\,n+5\right)\,A_{n}}{2^{6\,n}}} $$
(%i4) 32/%pi=sum(((42*sqrt(5)+30)*n+5*sqrt(5)-1)*'(A[n])/2^(6*n)*((sqrt(5)-1)/2)^(8*n),n,0,inf);
$$ \tag{%o4} \frac{32}{\pi}=\sum_{n=0}^{\infty }{\frac{\left(\sqrt{5}-1\right)^{8\,n}\,\left(\left(42\,\sqrt{5}+30\right)\,n+5^{\frac{3}{2}}-1\right)\,A_{n}}{2^{14\,n}}} $$
なんだか不思議な公式です。この1/π論文によれば、ウォルトディズニーの有名な映画の中に、この3つの公式のうち、%o2と%o3が登場する場面があるそうです。どの映画かは論文で確認してみてください。うちの娘達が結構気に入っていたので、私もみたことがあります。(これらの式には気がつきませんでした、、、残念)。
ラマヌジャンの論文ではこれらの3つに加えて合計17もの1/πに関する公式が提示されているそうです。ただしこれらの公式の証明に関しては、1928年にChowlaという数学者が上記%o2を証明したのですが、それ以降これらの式が議論されることはなかったそうです。
1/π論文はラマヌジャン系の公式を使ったπの多桁計算の話に移ります。
1985年に珍しいことが起こりました。Bill Gosperという数学者兼ハッカー(!)がラマヌジャンの17個の公式の中の一つ:
(%i5) 9801/(%pi*sqrt(8))=sum((4*n)!*(1103+26390*n)/((n!)^4*396^(4*n)),n,0,inf);
$$ \tag{%o5} \frac{9801}{2^{\frac{3}{2}}\,\pi}=\sum_{n=0}^{\infty }{\frac{\left(26390\,n+1103\right)\,\left(4\,n\right)!}{396^{4\,n}\,n!^4}} $$
を用いて、円周率\(\pi\)を1752万6100桁求めて、世界記録を樹立したのです。問題は当時17個の公式のうち証明されていたのはChowlaによる%o2だけで、%o5はまだ証明がなかったことにあったのです。ただしその直前まで記録を持っていた金田先生(東大の大型計算機センターにおられた有名な先生ですね)に計算結果を送り確認してもらい、両者はその部分までは完全に一致していたのだそうです。これで逆にラマヌジャンの公式%o5がほぼ絶対に正しいことが確信されたのでした。
この種の公式が円周率の多桁計算に用いられたこともあり研究が進み、以下の式がChudnovskyによって1988年に証明されたのだそうです。
(%i6) 1/%pi=12*sum((-1)^n*(6*n)!*(13591409+545140134*n)/((n!)^3*(3*n)!*(640320)^(3*n+3/2)),n,0,inf);
$$ \tag{%o6} \frac{1}{\pi}=12\,\sum_{n=0}^{\infty }{\frac{\left(545140134\,n+13591409\right)\,640320^{-3\,n-\frac{3}{2}}\,\left(-1\right)^{n}\,\left(6\,n\right)!}{n!^3\,\left(3\,n\right)!}} $$
この式、、、整理されていますが、冒頭に紹介したMorainの論文に掲載されていた公式にそっくりです。こいつは正しい式なのか、数値計算で検算してみましょう。最初の10項程度を取ります。
(%i7) ratsubst(10,inf,%);
$$ \tag{%o7} \frac{1}{\pi}=\frac{3\,\sum_{n=0}^{10}{\frac{\left(545140134\,n+13591409\right)\,\left(-1\right)^{n}\,\left(6\,n\right)!}{640320^{3\,n}\,n!^3\,\left(3\,n\right)!}}}{128\,10005^{\frac{3}{2}}} $$
そして、数値計算をしてみましょう。
(%i8) %,nouns,numer;
$$ \tag{%o8} 0.3183098861837907=0.3183098861837908 $$
見事右辺と左辺がほぼ一致しました。式はあっていそうです。
%o6とMorainの論文の式を見比べて、検討した結果、Morainの論文の式の右辺の分母に7が含まれているべきなのに入っていないことが確認できました。正しくは、
のようにすれば数値計算が一致することが確認できました。
さすがに15年前の論文にミスプリ指摘されても楽しくないでしょうから、この発見はMorainさんにはお知らせしないことにします、、、。