-Maxima入門- グラフ理論パッケージ、隣接行列、三角形の数

f:id:jurupapa:20150418081331j:plain
ハナミズキ

グラフ理論パッケージの使い方の続きです。

今回は行列、特にトレースを計算するmattrace()関数を使うので、準備としてnchrplパッケージも読み込んでおきます。
(%i1) load(graphs)$
(%i2) load(nchrpl)$

次にグラフを生成します。今回はランダムにグラフを生成する関数random_graph(n,p)を使ってみます。この関数の第一引数は頂点の数、第二引数は頂点同士を辺で結ぶかどうかを決める確率です。ここでは9頂点のグラフで確率0.4で辺を結ぶことにします。
(%i3) g1:random_graph(9,0.4);
$\tag{%o3} \verb|GRAPH(9 vertices, 14 edges)|$
それでは早速、描画してみましょう。
(%i4) draw_graph(g1,show_id=true,text_color=white);
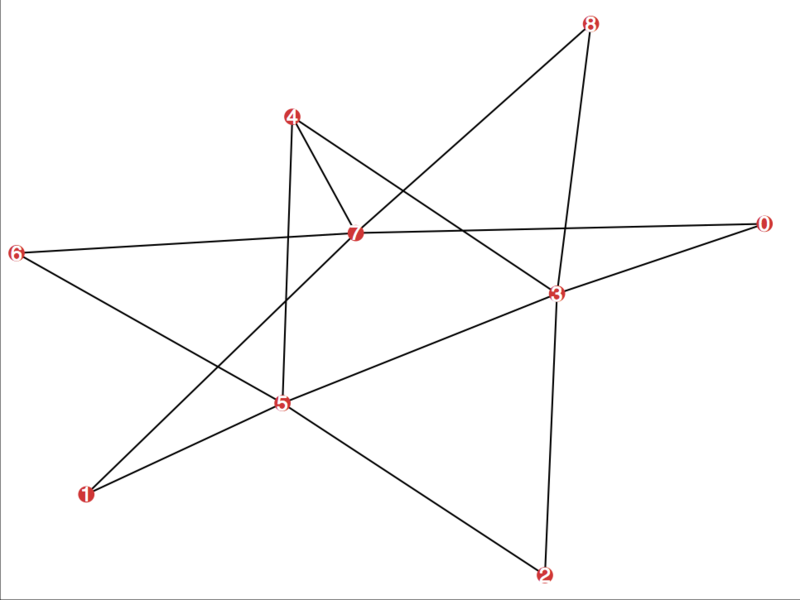[ f:id:jurupapa:20150501003053p:plain ,w400]
$\tag{%o4} \mathbf{done}$
この中に３角形は幾つあるか数えてみてください。

あるグラフに含まれる３角形の数を計算で求めることができます！！！
まずこのグラフの隣接行列を求めます。隣接行列はi,j要素が、頂点iと頂点jが辺で結ばれていれば1, 結ばれていなければ0となるような行列のことです。adjacency_matrix()関数で求めることができます。
(%i5) adjacency_matrix(g1);
$\tag{%o5} \begin{pmatrix}0&1&0&0&0&1&0&0&0\\ 1&0&1&0&1&0&0&1&1\\ 0&1&0&1&0&0&0&0&0\\ 0&0&1&0&1&1&1&1&0\\ 0&1&0&1&0&1&0&0&0\\ 1&0&0&1&1&0&1&0&1\\ 0&0&0&1&0&1&0&0&0\\ 0&1&0&1&0&0&0&0&0\\ 0&1&0&0&0&1&0&0&0 \end{pmatrix}$
一つ気をつけなければいけないことがあります。この行列、頂点iと頂点jの結線情報は右からi番目、下からj番目の要素を見る必要があります。上のグラフの描画と行列を見比べてみてください。

次に隣接行列の３乗を計算します。
(%i6) %^^3;
$\tag{%o6} \begin{pmatrix}0&8&1&5&1&8&1&1&0\\ 8&0&8&3&11&3&6&8&8\\ 1&8&0&8&1&5&1&0&1\\ 5&3&8&4&10&9&7&8&5\\ 1&11&1&10&2&10&2&1&1\\ 8&3&5&9&10&4&7&5&8\\ 1&6&1&7&2&7&2&1&1\\ 1&8&0&8&1&5&1&0&1\\ 0&8&1&5&1&8&1&1&0 \end{pmatrix}$