
御所車
(この本の17.7章には今回紹介している\( \Lambda(n) \) 関数についてのまとめがあり参考になります)。
数論的関数、と呼ばれる一群の関数があります。与えられた自然数nの約数の個数、nの約数の総和、n以下でnと既約な自然数の個数、、、これらは自然数nの関数として定義される数論的関数の例です。
さてマンゴールト関数も数論的関数なのですが、その定義はちょっと変わっています。ぶっちゃけ、この定義を初めて見て、「これは役に立つ素晴らしい関数だ!」と思う人はいないのではないでしょうか。まあ、定義を見てみましょう。
この関数は通常大文字のラムダ(Λ)で表されます。
\( \Lambda(n) \) は \( n = p^k \)となる素数pと自然数kが存在するならlog(p), それ以外のnに対しては0と定義されます。
Maximaで定義する場合、効率を考えず、定義に忠実に書くと以下のような感じでしょうか。factors_onlyというシステム変数の値をtrueに設定してifactors(N)を呼び出すと、Nの素因数がリストで得られます。リストの長さが1ならばnはその素因数の冪乗であることが分かります。
(%i1) mangoldt(N):=if integerp(N)
then block([fct],fct:ev(ifactors(N),factors_only:true),
if length(fct)=1 then log(fct[1]) else 0)
else 'mangoldt(N)$
以下は綺麗に出力するためのおまじないです。
(%i2) texput(nounify(mangoldt), "\\Lambda")$
では実際にいくつかの値を求めてみます。
(%i3) map(mangoldt,[1,2,3,4,5,6,7,8,9,10,11,12]);
$$ \tag{%o3} \left[ 0 , \log 2 , \log 3 , \log 2 , \log 5 , 0 , \log 7 , \log 2 , \log 3 , 0 , \log 11 , 0 \right] $$
4, 8, 9は素数の冪乗になっていること、6, 10, 12は複数の素因数を持つ合成数であることに注意して計算結果を見て下さい。
解析的数論の教科書を見ていると、マンゴールト関数もよく出てくるのですが、その総和もよく出てきます。以下がMaximaによる定義です。xを正の実数とします。
(%i4) psi0(x):=sum(mangoldt(n),n,1,floor(x));
$$ \tag{%o4} \mathrm{psi0}\left(x\right):=\mathrm{sum}\left(\mathrm{mangoldt}\left(n\right) , n , 1 , \left \lfloor x \right \rfloor\right) $$
このマンゴールト関数の総和は素数個数関数と同じように、x以下の素数と関連したステップ関数です。性質が非常に良く解析的に扱い易いため、ゼータ関数の研究ではこちらの方が素数個数関数よりもよく使われます。
グラフを描いてみます。
(%i5) wxplot2d([psi0(x),x],[x,2,200],[y,2,150]);
plot2d: some values were clipped.
plot2d: some values were clipped.
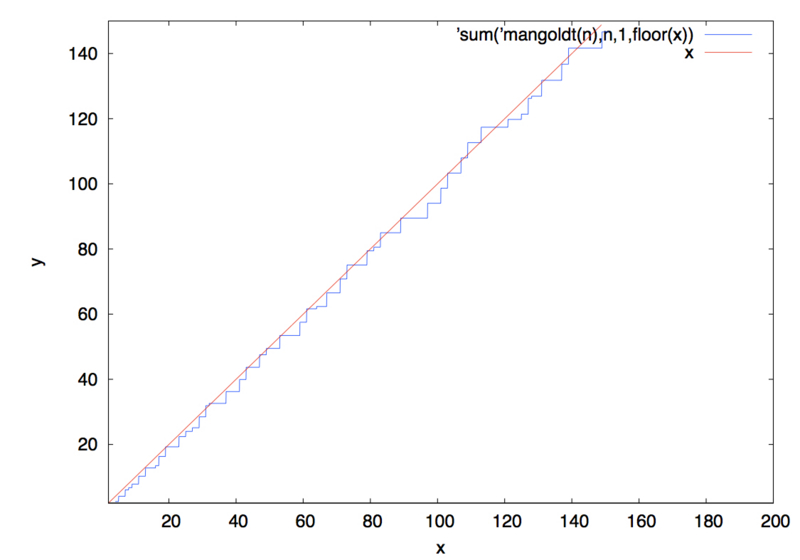
xが素数pの冪乗の時にlog(p)の高さの階段を上がっています。赤い線はy=xです。よく重なっていることがわかります。
$$ \tag{%o5} $$
