次は上記の本のp30に載っている練習問題(問題1.1)です。
実数x, yが下記の式El (%o2)を満たす時、x, yの動く範囲を求めよ。
早速やってみましょう。
(%i1) load("qepmax.mac")$
(%i2) El:3*x^2-4*x*y+6*y^2-8*x-4*y+3=0;
$$ \tag{%o2} 6\,y^2-4\,x\,y-4\,y+3\,x^2-8\,x+3=0 $$
xが存在するためのyの条件を求めるにはxに存在量化子をつけ、yを自由変数とします。
(%i3) qe([ [E,x] ],El);
$$ \tag{%o3} 2\,y^2-4\,y-1\leq 0 $$
念のためyについて解いて、見やすくします。
(%i4) rangey:solve(lhs(%),y);
$$ \tag{%o4} \left[ y=-\frac{\sqrt{6}-2}{2} , y=\frac{\sqrt{6}+2}{2} \right] $$
またyが存在するためのxの条件を求めるためにはyに存在量化子を付け、xを自由変数とします。
(%i5) qe([ [E,y] ],El);
$$ \tag{%o5} x^2-4\,x+1\leq 0 $$
こちらも同様、xについて解いて、見やすくします。
(%i6) rangex:solve(lhs(%),x);
$$ \tag{%o6} \left[ x=2-\sqrt{3} , x=\sqrt{3}+2 \right] $$
これらの結果をまとめてグラフに描いてみます。
(%i7) wxdraw2d(implicit(El,x,0,4,y,-1,3),explicit(rhs(part(rangey,1)),x,0,4),
explicit(rhs(part(rangey,2)),x,0,4),implicit(part(rangex,1),x,0,4,y,-1,3),
implicit(part(rangex,2),x,0,4,y,-1,3));
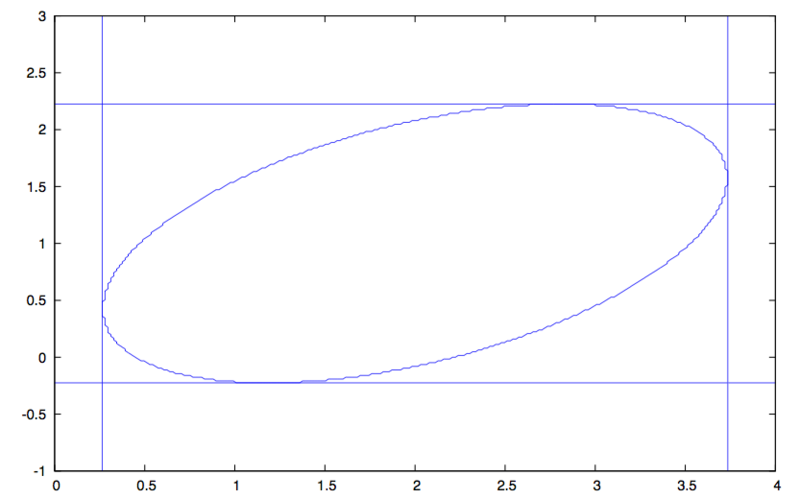
$$ \tag{%o7} \left[ \mathrm{gr2d}\left(\mathrm{implicit} , \mathrm{explicit} , \mathrm{explicit} , \mathrm{implicit} , \mathrm{implicit}\right) \right] $$
