この記事のコードをJupyter notebook形式で見るにはこちら。
素数個数関数に対するリーマンの明示公式で使用した\(J(x)\)関数の第1項が素数の位置を正確に知っている、というお話しをしました。この項がゼータ関数の非自明零点からの貢献になっています。ただその計算には複素関数としての対数積分関数が登場し、計算には工夫が必要でした。
実は、ゼータ関数の非自明零点が素数の位置を知っている、ということに関して対数積分関数は本質的なものではありません。第1項をずっと簡素化した(%o1)のような式を考えてみましょう。
(%i1) f(x)='realpart(sum(x^rho[j],j,1,inf));
$$ \tag{${\it \%o}_{1}$}f\left(x\right)={\it realpart}\left(\sum_{j=1}^{\infty }{x^{\rho_{j}}}\right) $$
\(\rho_j\)はj番目の非自明零点を表します。対数積分関数はもうありません。随分と簡素化してしまいましたが、この\(f(x)\)もしっかりと素数の位置を知っています。実際に計算してみましょう。
(%i2) /*
The LMFDB Collaboration, The L-functions and Modular Forms Database,
home page of the Zeros of zeta(s),
https://www.lmfdb.org/zeros/zeta/?limit=200&N=1, 2020 , [Online; accessed 10 October 2020].
*/
kill(img_rho);
img_rho:[
14.1347251417346937904572519835625,
21.0220396387715549926284795938969,
25.0108575801456887632137909925628,
30.4248761258595132103118975305840,
32.9350615877391896906623689640747,
途中省略。合計200個の零点をダウンロードしました。この計算のipynbファイルはすべての零点を含んでいます。
388.8461283542322546008094203003735,
391.4560835636380457705782281225541,
392.2450833395190967490151841709930,
393.4277438444340259366989529201288,
395.5828700109937209708777113231417,
396.3818542225921869319994544917305
]$
$$ \tag{${\it \%o}_{2}$}\mathbf{done} $$
\(\rho_j=\frac{1}{2}+\%i \, img\_rho[j]\)です。また非自明零点は200個足します。これらを代入してMaximaで計算できるように関数を定義します。
(%i4) f(x):=-ev(realpart(sum(x^(1/2+%i*img_rho[j]),j,1,200)),numer);
$$ \tag{${\it \%o}_{4}$}f\left(x\right):=-{\it ev}\left({\it realpart}\left({\it sum}\left(x^{\frac{1}{2}+i\,{\it img\_rho}_{j}} , j , 1 , 200\right)\right) , {\it numer}\right) $$
比較のために数え上げによる方法で素数個数関数\(\pi(x)\)を定義します。
(%i??) pi1[n]:=if n<2 then 0 elseif primep(n) then pi1[n-1]+1 else pi1[n-1]$
(%i??) pi(x):=if integerp(x) and primep(x) then pi1[x]-1/2 else pi1[floor(x)]$
ではグラフにプロットしてみましょう。\(f(x)\)は青、\(\pi(x)\)は赤い線です。
(%i7) plot2d([f(x),pi(x)*10],[x,1,100]);
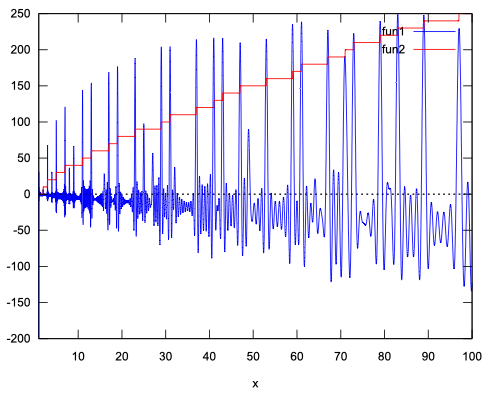
何が起こっているかわかりますか。素数個数関数\(\pi(x)\)がジャンプするところ、すなわち\(x\)が素数の時、\(f(x)\)に高いスパイクが立っていることが見て取れます(低いスパイクは無視してください)。\(f(x)\)の定義は、
$$ f\left(x\right)={\it realpart}\left(\sum_{j=1}^{\infty }{x^{\rho_{j}}}\right) $$
でした。例えばグラフの30〜40の区間を見てください。\(x\)を例えば31と決めて、200個の非自明零点\(\rho_j\)について\(31^{\rho_j}\)を計算して足し合わせると、高いスパイクが立ちますが、\(x\)=32〜36について\(x^{\rho_j}\)を計算してたし合わせても、高いスパイクは立たちません。\(37^{\rho_j}\)を足し合わせると、また高いスパイクが立つわけです(31は素数、32,33,34,35,36は合成数、37は素数)。
と言うわけで、ゼータ関数の非自明零点\(\rho_j\)は素数の位置をよく知っているわけです。
\(f(x)\)は実はvon Mangoldt関数ととても深く関係しています。その辺の話はかなり昔に、以下の記事で書いています。グラフに低いスパイクが立つ時の\(x\)についても書いてあります。
以下は参考にした文献です。
[1] Conrey, The Riemann Hypothesis https://www.ams.org/notices/200303/fea-conrey-web.pdf
[2] The LMFDB Collaboration, The L-functions and Modular Forms Database,
home page of the Zeros of zeta(s),
https://www.lmfdb.org/zeros/zeta/?limit=200&N=1, 2020 , [Online; accessed 10 October 2020].