
佐藤テイト予想が成立するためには「虚数乗法を持たない楕円曲線に対して」という条件が付いていました。もう一度楕円曲線版の佐藤テイト予想・テイラーの定理を再掲します。
佐藤テイト予想・テイラーの定理
虚数乗法を持たない楕円曲線Eに対して、法pでの解の個数をNsolve(E,p)とする。
$$ \frac{\left| \mathrm{\%Nsolve}\left(E , p\right)-p \right| }{2\,\sqrt{p}}=\cos \vartheta_{p} $$
となる\( \vartheta_{p} \)は様々な値をとるが、\( \frac{2}{\pi}\,sin ^2x \)という形で分布する。
当然の疑問として虚数乗法を持つ楕円曲線ではこの分布はどうなるのでしょうか。虚数乗法を持つ楕円曲線を一つ例にとり、実際にグラフを描いてみます。例で使う楕円曲線 \( y^2+y=x^3-7 \)はwww.lmfdb.orgで見つけたものです。
まずは色々と準備です。
(%i1) load("qsexpand.lisp")$
(%i2) Nsolve(elc,p):=block([c:0,evelc],
for x:0 while x<p do
for y:0 while y<p do
(evelc:ev(elc), if 0=mod(rhs(evelc)-lhs(evelc),p) then c:c+1),
return (c))$
(%i3) NsolveF(elc,p):=(elc:ev(elc,nouns),if lhs(elc)#y^2 or p=2 or p=3 then Nsolve(elc,p) else sum(1+ev(jacobi(rhs(elc),p),nouns),x,0,p-1))$
(%i4) powerdisp:false;
$$ \tag{%o4} \mathbf{false} $$
例として使う楕円曲線を定義します。
(%i5) elc:y^2+y=x^3-7;
$$ \tag{%o5} y^2+y=x^3-7 $$
左辺を有限体\(F_p\)で平方完成するための道具も定義します。
(%i6) sq_complete(poly,var,p):=
block([c2,c1,c0],c2:coeff(poly,var,2),
c1:coeff(poly,var,1),c0:coeff(poly,var,0),
c2*(var+c1*'inv_mod(2*c2,p))^2+c0-c1^2*'inv_mod(4*c2,p))$
ではelcを平方完成します。
(%i7) sq_complete(lhs(elc),y,p)=rhs(elc);
$$ \tag{%o7} \left(\mathrm{\%inv\underline{\quad}mod}\left(2 , p\right)+y\right)^2-\mathrm{\%inv\underline{\quad}mod}\left(4 , p\right)=x^3-7 $$
(%i8) %-second(lhs(%));
$$ \tag{%o8} \left(\mathrm{\%inv\underline{\quad}mod}\left(2 , p\right)+y\right)^2=x^3+\mathrm{\%inv\underline{\quad}mod}\left(4 , p\right)-7 $$
新左辺を\( y^2 \)と置き直します。
(%i9) elc2:y^2=rhs(%);
$$ \tag{%o9} y^2=x^3+\mathrm{\%inv\underline{\quad}mod}\left(4 , p\right)-7 $$
実際に多数の素数について\( \theta_p \)を計算する関数を定義します。
(%i10) sato_tate(elc,minp,maxp):=block([res],
res:[ ],
for p:next_prime(minp-1) next next_prime(p) thru maxp do
res:append([acos((p-NsolveF(elc,p))/(2*ev(sqrt(p),numer)))],res),
res)$
elc2に対して、1〜1000までの素数について\(\theta_p\)を計算します。
(%i11) res:sato_tate(elc2,1,1000)$
(%i12) load(draw)$
(%i13) load(descriptive)$
ヒストグラムを描画します。
(%i14) draw2d(proportional_axes=xy,
histogram_description(res,nclasses=20,frequency=density),
explicit(2/%pi*sin(x)^2,x,0,%pi),xrange=[0,%pi])$
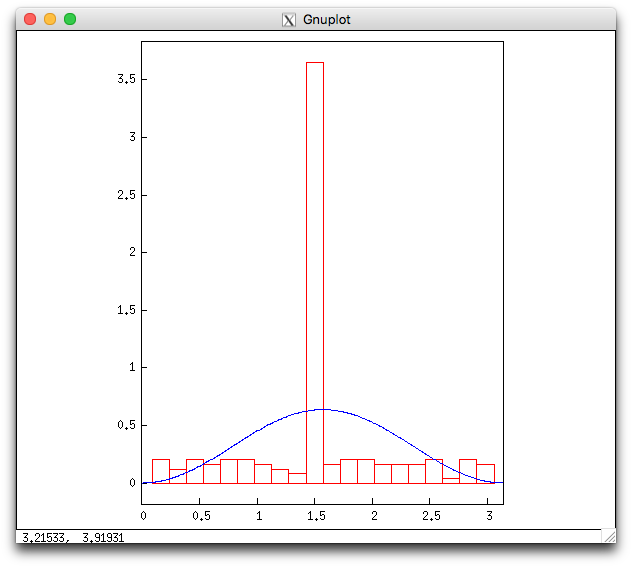
全く重なりません。文献によればこの場合、非常に多くの素数pについて\(F_p\)での解の個数はpと一致するためその差が0となり、\(\mathrm{arcsin}\left(0\right)=\frac{\pi}{2}\)となるため、\(\frac{\pi}{2}=1.5707 \)であるため上記のグラフになるそうです。
The LMFDB Collaboration, The L-functions and Modular Forms Database, Modular Form 27.a3, http://www.lmfdb.org/EllipticCurve/Q/27/a/3, 2016, [Online; accessed 18 June 2016].